ObrevierGrafiken

Tools
Obertonbrevier
Soundbeispiele
Tuvas
Noten
Buchtips
CD-Tips
ARS NOVA
Weblinks
www.oberton.info

Hier kommentarlos einige Sachverhalte zu experimentieren, daß heißt zur Visualisierung oder Komposition von neuer Musik.

Die (Quinten)-Klangspiralen

Grafik: Klangspirale über einen Tonraum von 5 Oktaven

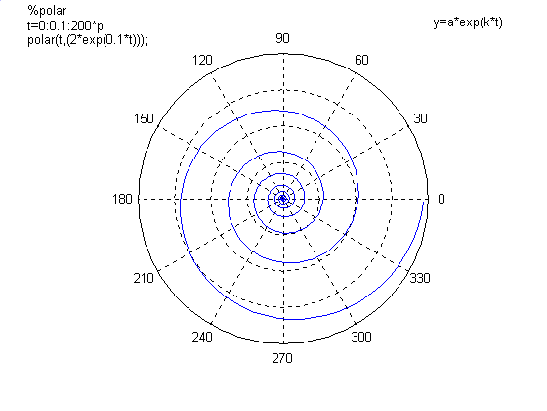
Grafik: Logarithmische Spirale des Quintenzirkels

Formeln für die Spiralberechnung polar und kartesisch

Die Formel für die logarithmische Spirale in Polarkoordinaten lautet
r = a*e^kj , wobei jede Gerade, die durch den Ursprung geht die
logarithmische Spirale unter demselben Winkel t0 schneidet.
t0 = arccot k. Die Tangenten an diesen Schnittpunkten sind einander parallel.
r ist der Radius der Spirale bis zum Schnittpunkt, e ist die Eulerzahl mit einem
Wert von 2.7182818...

Für die Umrechnung von Polarkoordinaten in kartesische
Koordinaten gilt die Beziehung:

x = r cos j, y = r sin j Die Darstellung in Polarkoordinaten macht sich besser.

Ist r = r ( j ) die Darstellung der Funktion in Polarkoordinaten, kann man aufgrund o.g. Beziehung zwischen Polar- und kartesischen Koordinaten, zu einer Parameterdarstellung der Funktion mit dem Parameter j
übergehen: x = r ( j ) cosj, y = r ( j ) sinj

Grafik von 5 hintereinandergelegten Oktaven

Etwas zur haromonice mundi von Kepler:

Die Planetentonreihen nach Kepler
Planet	Planetentonreihe	Schlüssel
Saturn	G, A, H, A, G	Bass
Jupiter	G, A, B, A, G	Bass
Mars	f, g, a, b, c', h, a, g, f	Bass
Erde	g', b', g'	Violin
Venus	e'', e'', e''	Violin
Merkur	c', d', e', f ', g', a', h', c'', d'', e'', c'', g, e, c'	Violin
Hic locum habert etiam	g', a', h', c'', a', g'	Violin

Etwas zum Tonfarbenkreis von Goethe:

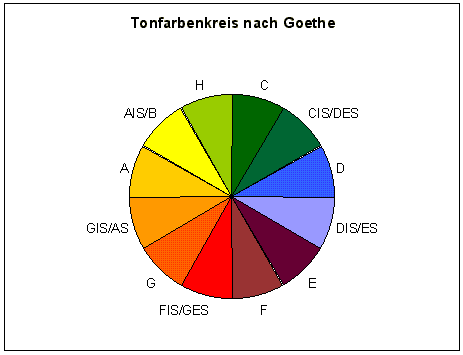
Wer bis hierhin durchgehalten hat, kann letztlich noch einen sehr schönen Artikel Über Obertonmusik von Markus Riccabona lesen.