Tools
Obertonbrevier
Soundbeispiele
Tuvas
Noten
Buchtips
CD-Tips
ARS NOVA
Weblinks
www.oberton.info

Das kleine Obertonbrevier

Inhalt:

1. 1.1 1.1.0 1.1.1 1.2 2. 4. 4.1 5. Das Phänomen der Obertonreihe - Grundlage der Harmonielehre
Schwingungsverhätnisse der Teiltonreihe (Partialtonreihe)
Teiltöne, Frequenzverhältnisse und Intervallproportionen
Zerlegung der Teiltonreihe durch Fouriertransformation
Ableitung eines harmonischen Tonsystems aus der Teiltonreihe
1.3 Berechnung der Anzahl der Teiltöne pro Oktavstreifen
1.4 Kleiner Exkurs über die Hintergründe unseres Tonsystems
Akustik der menschlichen Stimme und Sprache mit Einschub
2.1 Die Formatregionen der Konsonanten und Vokale
2.2 Obertonsänger von Tuwa (Spektrum der Wissenschaft)
3. Die Synthese von Vokalen und das Vokaldreieck
3.1 Die Sprachmelodie und ihre Wirkung auf die menschliche Seele
Das System der sechs Grundübungen des Obertonsingens
Übungen zum Obertongesang nach Michael Vetter
Literaturliste, Discographie
ANHANG:
Berechnungsformeln für Obertöne, Tabellen und Grafiken
Berechnung der Anzahl von Obertönen pro Oktavraum
Berechnung der Frequenz eines Tones nach Intervallsprung
Berechnung von Intervallen in Centwerten
Kleiner Exkurs zur Beschreibung verschiedener Tonsysteme
Das phythagoräisch Diatonische Tonsystem
Die Entwicklung des modernen europäischen Tonsystems
Ableitung der reinen harmonischen diatonischen 7-Tonleiter
Die Temperatur
Quintenspiralen, Tonfarbenkreis (Goethe), Planetentöne (Kepler)u. Spiralberechnung
Viele Stimmen aus einer Kehle (Markus Riccabona)

1. Das Phänomen der Obertonreihe - Grundlage der Harmonielehre

Zupft man eine Saite eines beliebigen Saiteninstruments an und bringt diese so zum Klingen, so nimmt man zusammen mit dem Grundton, der am lautesten erklingt, eventuell noch eine ganze Reihe von Obertönen wahr, die jedoch meistens eher als Klangfarbe empfunden werden. Die Summe dieser Töne, Grundton und Obertöne, bilden also zusammen den Klangcharakter dieses Tones. Die Obertöne sind in dem Klang jeder natürlichen Tonquelle enthalten und prägen im wesentlichen die Klangfarbe des Instruments, der menschlichen Stimme oder des Tonerzeugers. Von diesen Obertönen gibt es unzählige. Für die Belange unseres Tonsystems und der Skalen-Akkord-Harmonik unseres Jahrhunderts sind jedoch nur die ersten15 Obertöne relevant. Wenn man den Grundton zu den 15 Obertönen dazunimmt, erhält man eine Reihe von 16 Tönen, die als "Teiltonreihe" bezeichnet wird.

Der siebente, elfte, dreizehnte und vierzehnte Partialton erklingen nicht genauso wie im europäischen gleichschwebend temperiertem Tonsystem, sondern tiefer oder höher. Dies macht den magisch mystischen Reiz der gesungenen Obertöne aus. Zwischen dem 16. und dem siebzehnten Partialton beginnt, daß die Intervalle kleiner als ein Halbtonschritt werden, und ab dem 48. Teilton sind die Tonunterschiede zwischen den aufeinanderfolgenden Tönen kaum noch wahrnehmbar. Ja, sie verschmieren sozusagen zu einem Band. Auch das macht akustisch einen besonderen Reiz aus.
Wie auf der folgenden Grafik zu erkennen, addiert sich die Grundfrequenz (Schwingungen pro Sekunde) von Teilton zu Teilton. Dieser lineare Zusammenhang (siehe weiter unten) äußert sich aber beim Hörvorgang nicht in der Weise, daß der Ton immer um einen bestimmten Betrag höher wird, sondern hier ist der Zusammenhang logarithmisch

1.1 Schwingungsverhätnisse der Teiltonreihe (Partialtonreihe)

Das Verhältnis des 4:5:6 Teiltons ergibt den Durdreiklang des 1. Partialtons, auch Zeugerton oder Grundton genannt (hier D : Fis : A), wohingegen der Molldreiklang entweder in der sogenannten Untertonreihe zu suchen wäre (dann aber auch von oben nach unten aufgebaut wäre 6:5:4 = D: B : G), die sich genau spiegelbildlich zur Obertonreihe verhält und im Gegensatz zur harmonischen Teilung die arithmetische Teilung erfährt (Die "Dualisten": Zarlino, von Öttingen, Riemann), oder in einem Verhältnis der Obertonreihe, wo die Teiltöne nicht wie im Dur beieinander liegen (10:12:15).(Mehr hierzu siehe bitte den ANHANG!
Die elektronisch erzeugten Untertöne sind in Deutschland erstmals 1930 am Trautonium nachgewiesen worden. Hierzu ein interessanter Link: http://www.deutsches-museum-bonn.de und ein Tonbeispiel der subharmonischen Teiltöne erzeugt mit dem Mixturtrautonium von Sala: Subharmonische

Aber es geht auch anders, nämlich indem man mit einem Blatt Papier seitlich eine schwingende Stimmgabel berührt. Die Schwingungen werden übertragen, lassen das Papier aber als Platte schwingen. Die Geometrie der schwingenden Platte und die Trägheit lassen Töne enstehen, die auch in der Untertonreihe enthalten sind. Ändert man den Berührungspunkt der Stimmgabel am Papier, ändern sich auch die erklingenden Töne und man kann Tonreihen entstehen lassen, wie z. B. den oben erwähnten Molldreiklang. Jedoch ist nicht erwiesen, ob es sich hier nur um eine nichtlineare Verzerrung der Obertöne, oder um wahre Untertöne handelt. Chladni hat ja auch mit schwingenden Platten gearbeitet und schöne geometrische Muster auf gleiche Weise erzeugt, wie hier die Töne (durch Induktion) erzeugt werden.

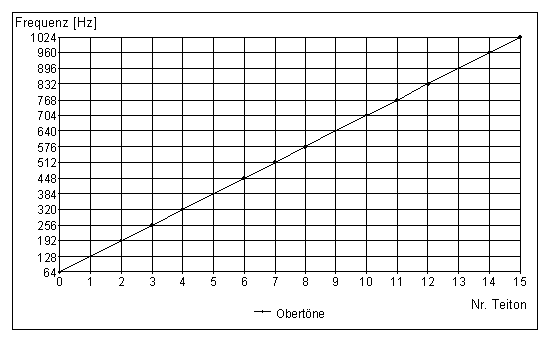
Auch die Untertonreihe ist unbegrenzt: sie führt zu immer tieferen Schwingungen mit immer langsamerem Rhythmus, und weist letztendlich in die Zeitlosigkeit.

Grafik 1: Frequenz eines Tons in Abhängigkeit der Stellung in der Obertonreihe (gilt auch für die Untertonreihe, nur reziprok)

1.1.0 Die Teiltöne, ihre Frequenzverhältnisse und Intervallproportionen

Der Grundton "D" im Beispiel ist somit der erste Teilton dieser Teiltonreihe; der erste Oberton "d" ist demnach als der zweite Teilton dieser Teiltonreihe anzusehen. Das Frequenzverhältnis dieser, in einem Abstand einer Oktave liegenden, Töne beträgt 1:2.
Die Schwingungen eines Tones pro Sekunde ("Frequenz") werden nach dem deutschen Physiker Heinrich Hertz mit "Hertz" bezeichnet. Hat der Grundton beispielsweise eine Frequenz von 64 Hertz, was bedeutet, daß die Luft 64 mal im Verlauf einer Sekunde verdichtet wird, während der Tonerzeuger schwingt (Stimmbänder, Saite, etc.), so hat der erste Oberton eine Frequenz von 128 Hertz. Er liegt genau eine Oktave höher. Der dritte Teilton hat die dreifache Frequenz vom Grundton (192 Hertz). So hat demnach jeder folgende Teilton vom vorhergehenden Ton einen gleichbleibenden Abstand von 64 Hertz. Die obige Grafik zeigt das Verhältnis der Obertonreihe zu den jeweiligen Frequenzwerten an. Auf der waagerechten Achse sind die 16 Teiltöne aufgetragen, auf der senkrechten die entsprechende Anzahl der Schwingungen pro Sekunde. Die Gerade zeigt die Funktionale Abhängigkeit zwischen Frequenz und Teiltönen. Der Zusammenhang ist linear.

Die jeweilige Nummer eines Teiltons verrät uns auch, an welcher Stelle man eine einzelne Saite durch Auflegen (nicht Abgreifen) eines Fingers teilen muß, um die jeweiligen Töne der Obertonreihe erklingen zu lassen. Ein Instrument, was diese Gegebenheit nutzt ist das Trumbscheid (Tromba Marina, Monochord). Als Demonstartionsobjekt der Teilungsverhältnisse diente bereits den alten Griechen zu Zeiten Pythagoras' das Monochord, ein antikes Instrument, was zu Lehrzwecken diente, mit nur einer Saite. So muß man die Saite genau in der Mitte teilen, um den ersten Oberton, die Oktave erklingen zu lassen. Der gegriffene Ton steht also zur leeren Saite in einem Verhältnis von 2 :1. Die Oktave ist der zweite Teilton und kommt mit der Hälfte der Saitenlänge aus. Der dritte Teilton benötigt nur noch ein Drittel der Saitenlänge, der nächste nur noch ein Viertel usw., bis hin zum dreigestrichenen c, das mit nur einem Sechzehntel der Saitenlänge auskommt.
Es zeigt sich, daß das Teilungsverhältnis der Saite sich umgekehrt proportional zur Frequenz verhält. Greift man zum Beispiel ein Drittel der Saite ab und zupft die restlichen zwei Drittel an (2 : 3), so erklingt die Quinte zum Grundton, die die anderthalbfache Frequenz des Grundtons aufzuweisen hat (1,5 : 1). Oder greifen wir ein Viertel der Saite ab und lassen drei Viertel frei schwingen (3 : 4), so erklingt die Quarte, deren Frequenz zum Grundton in einem Verhältnis 1, 333 : 1 steht. DieTeilungsverhältnisse einer Saite zur Bestimmung der Intervalle werden Intervallproportionen genannt.
Die Obertonreihe kann also als die eigentlich "natürliche" Tonleiter aller Musik aufgefasst werden und wird auch Naturtonreihe genannt. Die im ersten Beispiel abgedruckte Reihe würde entstehen, wenn man ein auf D gestimmtes ventilloses Horn anbläst oder auf einem beliebigen Saiteninstrument auf einer Saite, die auf D gestimmt ist, die Flageolett-Töne erzeugt. Dies sind Töne, die durch leichtes Auflegen eines Fingers an einem bestimmten Teilungspunkt (z.B. die Hälfte, ein Viertel, oder Fünftel der Saitenlänge) entstehen. Auf einer Gitarre beispielsweise lassen sich die ersten fünf dieser Flageollett-Obertöne nacheinander am 12., 7., 5., 4. und 3. Bund erzeugen. Noch besser geht dies auf einem elektrischen Bass mit ungeschliffenen Saiten zu realisieren - auf diesen Saiten lassen sich fast alle der ersten 15 Obertöne hörbar machen.